RSA Algorithm

RSA (Rivest–Shamir–Adleman) was one of the first public key cryptosystems and is widely used to securely send messages over the internet. The implementation of RSA makes heavy use of modular arithmetic, Euler's theorem, and Euler's totient function that we have explained on the previous pages. The idea is that we choose n = pq, choose e with gcd(e, 𝜙(n)) = 1, and find d with ed ≡ 1 (mod 𝜙(n)). To encipher: P → E(P) ≡ P^e (mod n), where P denotes the plaintext and E denotes encrypt. To decipher: Q → D(Q) ≡ Q^d (mod n), where Q denotes the ciphertext and D denotes decrypt. To encode we need to know (n, e) and to decode, we need to know (n, d). Key Generation First, the receiver chooses two large primes p and q. The product n = pq forms half of the public key. We then use the totient function on n, denoted 𝜙(n),

If we know n and 𝜙(n), we can determine p and q. Rearranging the above equation, we get This can be written in the form of a polynomial: Example: Let n = 187 and 𝜙(n) = 160. Determine p and q. From the question we know, pq = 187 so p + q = 187 + 1 -160 = 28. Rewriting this as a polynomial, Using the quadratic function, we obtain the roots; x = (28 ± √28² - 4(1)(187)) / 2 = (28 ± √784; - 748) / 2 = (28 ± √36) / 2 = (28 ± 6) / 2 = 17, 11 So p = 11, q = 17. Finding the Decryption Key For the purpose of this example we’ve chosen very small primes but for encryption to be secure, remember you must choose large primes. Let And multiply to find n, the modulus We then choose e, which must be between 1 and 𝜙(n), and coprime to 𝜙(n), i.e. gcd(e, 𝜙(n)) = 1. Let; The decryption key, d, is such that This can be calculated using the extended Euclidean algorithm. 288 = (61 x 4) + 44 61 = (44 x 1) + 17 44 = (17 x 2) + 10 17 = 10 + 7 10 = 7 + 3 7 = (3 x 2) + 1 1 = 7 - 2(3) = 7 - 2(10 - 7) = 3(7) - 2(10) = 3(17 - 10) - 2(10) = 3(17) - 5(10) = 3(17) - 5[44 - 2(17)] = 13(17) - 5(44) = 13(61 - 44) - 5(44) = 13(61) - 18(44) = 13(61) - 18[288 - 4(61)] = 85(61) - 18(288) When compared to the earlier formula de ≡ 1 mod 𝜙(n), you can see that the coefficient of e = 61 is 85, the decryption key. Now we understand how to find the decryption key, let’s try to decrypt a secret message. We will assume that each letter of the alphabet has been given a number, i.e. A = 01, B = 02,..., Z = 26. Example: Your public key is (n,e) = (2173, 3) where n = 2173. You receive the message 1865 0183 1955 0308 0034 2130 0530 What does it say and what decryption exponent did you use? (n, e) = (2173, 3) where n = 2173 = 41*53 (p*q) P → E(P) ≡ P^e (mod n) ≡ P³ (mod 2173) To decode, we need (n, d) = (2173, d) where ed ≡ 1 mod 𝜙(n), 3d ≡ 1 (mod 𝜙(2173)). 𝜙(n) = (p - 1)(q - 1) 𝜙(2173) = (41 - 1)(53 - 1) = (40)(52) = 2080 3d ≡ 1 (mod 2080) 3d ≡ 1 + 2080k 1 = 3d - 2080k gcd(2080, 3) 2080 = 3(693) + 1 1 = 2080 + (-693)3 Therefore, d = -693 = -693 + 2080 (to make d positive add the modulus to the negative number) = 1387 D(E(P)) = 1865¹³⁸⁷ 0183¹³⁸⁷ 1955¹³⁸⁷ 0308¹³⁸⁷ 0034¹³⁸⁷ 2130¹³⁸⁷ 0530¹³⁸⁷ (mod 2173) P = 2015 1815 1420 1509 1903 1512 0424 = T O R O N T O I S C O L D X = Toronto is cold Encryption The formula you need for encryption in RSA is Where C is the ciphertext, M is the plaintext message, e is a number coprime to (which must be between one and 𝜙(n), non-inclusive) and n is the modulus. If you are working out an RSA encryption by hand, you will find that you can’t calculate on your calculator x⁶¹, therefore, you have to expand your expression using several laws of indices. As 61 is a prime number, this cannot be simplified into factors. However, 𝑥⁶⁰ can be simplified by finding its factors. 60 = 10 x 6 = 5 x 2 x 6 = 5 x 3 x 2 x 2 using prime factorisation By inserting the expression for 𝑥⁶⁰ into the expression for 𝑥⁶¹ you have the following: NOTES After each step you should be applying the modulus, as shown in the image below. 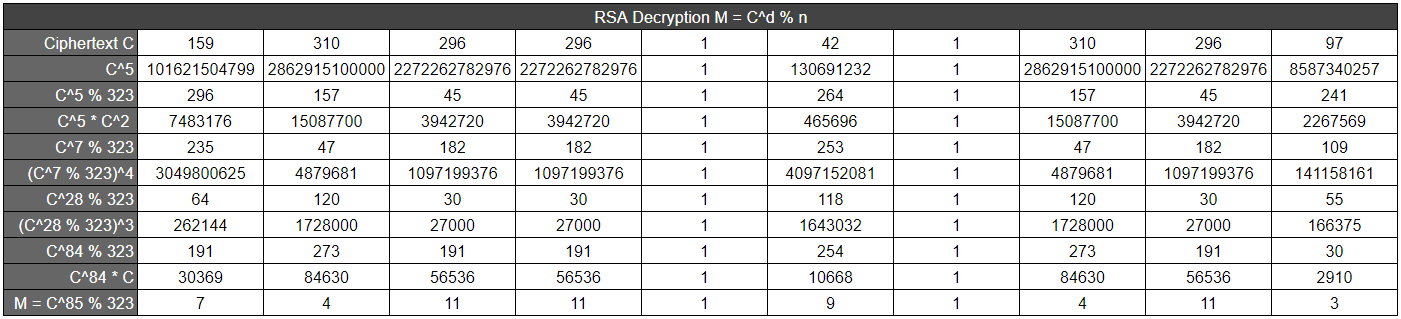𝑥^mn = (𝑥^m)ⁿ [Solve 𝑥^m first, then multiply the result by itself n times] 𝑥^m+n = 𝑥^m*𝑥ⁿ [Solve 𝑥^m and 𝑥ⁿ individually and multiply the results together] In the image below [(M⁵)⁴]³ was possible to calculate and quicker than {[(M⁵)³]²}² Decryption The decryption formula is The decryption can be worked out using the same method as before, but using d, the decryption key and not e. d is the multiplicative inverse of e mod 𝜙(n). Where d = 85, 85 = [(5 + 2) x 4 x 3] + 1, therefore

Written by Chelsea and JaneW