Diffie Hellman

The Diffie Hellman Key Exchange resolves the issue surrounding secure key transmission; using this method the key is never in the public domain. This method is used in conjunction with RSA and ECC, as well as other encryption methods. Alice and Bob agree on a Generator G in the public domain. They can then separately choose their private keys, which are not shared at all. Their private keys and the generator can then be used to find their public keys, which can be shared publicly. This concept is commonly explained using a colour metaphor, which we have used here to help visualise the operations performed to find the key. 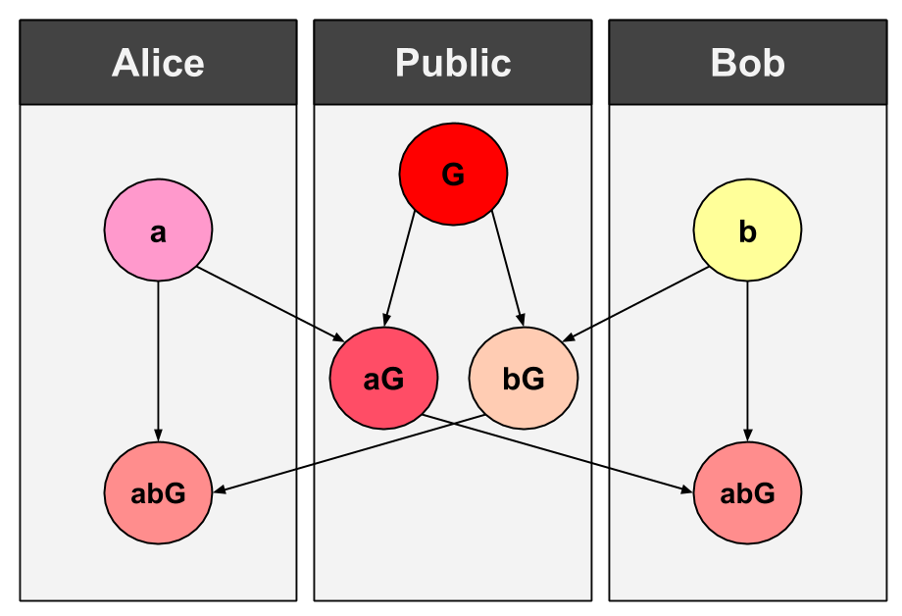In the image above you can see that Alice and Bob have shared their public keys aG and bG respectively. An interceptor would not be able to work out their private keys from their public keys as the mathematics are easy one way but extremely difficult to reverse. The key abG is then found with a private key and the public key of the person you are communicating with. A private key is required to find the key so nobody in the public domain can find the key from any of the public parameters of the encryption. Example: In public Alice and Bob agree on a large prime p and a primitive root of p, g. In this example we will use p = 7 and g = 3. Private keys are chosen such that a, b < p. In this example we will use, a = 2 and b = 4. The following formula is used to calculate a public key where x is the private key:

Alice’s public key: A = g^a mod p A = 3² mod 7 A = 9 mod 7 A = 2 Bob’s public key: B = g^b mod p B = 3⁵ mod 7 B = 243 mod 7 B = 5 The shared key can then be calculated using the following formulae: Alice calculates: K = B^a mod p K = 5² mod 7 K = 25 mod 7 K = 4 Bob calculates: K = A^b mod p K = 2⁵ mod 7 K = 32 mod 7 K = 4 It is important to note that this method is vulnerable to a man-in-the-middle attack. If an interceptor, Eve, calculates her own public key and is able to intercept the exchange of Alice and Bob’s private keys she can establish two different keys with Alice and Bob none the wiser. Alice will calculate a key with the public key provided by Eve, thinking it is Bob’s public key and Bob will do the same but they will now end up with different keys and will be unable to decrypt each other’s messages. Eve however has the capability to decrypt messages from either party and then re-encrypt the message with the key shared with the recipient. This way the message still reaches its destination but it has been viewed by Eve without the knowledge of either party. The integrity of the message is now in question also, as Eve can change the message before sending it on if she so decides. In the image below we use the colour metaphor again to help you visualise the man in the middle attack. 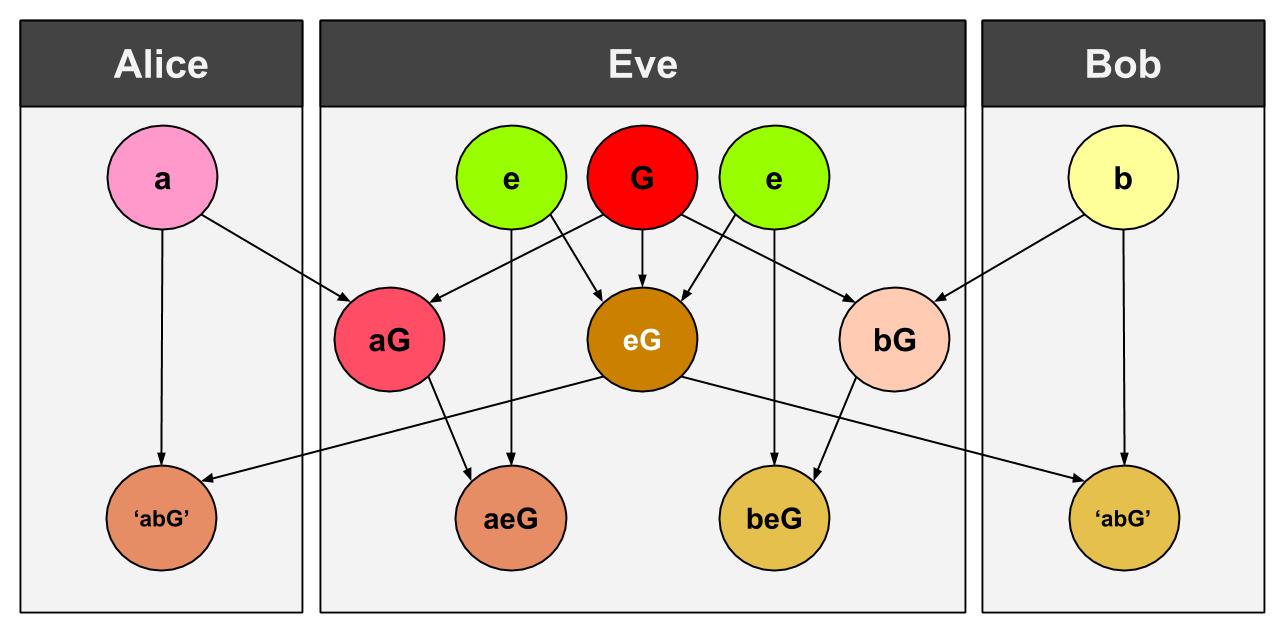Written by Chelsea