A basic cryptosystem model involves the encryption of plaintext, from a sender, using an algorithm, into ciphertext and then the decryption of the ciphertext into plaintext by the receiver. The goal of the cryptosystem is to send a message to a recipient without an interceptor or eavesdropper being able to extract the information.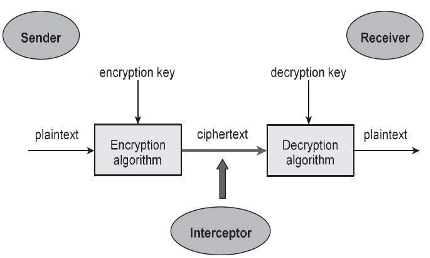
In order to ensure secure communication, the cryptosystem has key components including;
• Plaintext - The data to be protected during transmission or storage such as a text file, video message, image file, etc. It is usually denoted by M, for message, or P, for plaintext. The computer views M as binary data, a series of ones and zeros.
• Encryption Algorithm - Mathematical process, denoted by E, that produces a ciphertext for any given plaintext and an encryption key.
• Ciphertext - A scrambled version of the plaintext produced by the encryption algorithm using a specific encryption key. The ciphertext can be intercepted or compromised as it is sent on public communication channels, therefore anyone could access the information. It is denoted by C and stored as binary data on the computer.
The encryption algorithm E operates on M to produce C, which in mathematical notation can be written as:
E(M) = C
•
Decryption Algorithm - Mathematical process, denoted by D, that produces the original, unique plaintext for any given plaintext and a decryption key.
Hence, in the reverse process, decryption algorithm D operates on C to produce M:
D(C) = M
Since the decryption algorithm reverses the process of the encryption algorithm, the two algorithms are closely related, and the following identity must hold true:
D(E(M)) = M
In order for encryption/decryption algorithms to be widely useable, whilst maintaining secrecy, modern cryptography uses a key for both encryption and decryption denoted by K. For a given cryptosystem, the collection of all possible key values is called the keyspace.
•
Encryption Key - A value known to the sender that inserted into the encryption algorithm along with the plaintext to produce the ciphertext.
•
Decryption Key - Related to the encryption key but not always identical, it is a value known to the recipient that inserted into the encryption algorithm along with the ciphertext to produce the plaintext.
Using a key, the mathematical functions become:
EK(M) = C
DK(C) = M
These functions have the property:
DK(EK(M)) = M
If the algorithms use a different encryption and decryption key, the functions can be written as follows, denoting the separate keys as K1 and K2:
EK1(M) = C
DK2(C) = M
DK2(EK1(M)) = M
One of the main issues regarding a cryptosystem is an interceptor, or attacker. They are an unauthorised entity who attempts to determine the original plaintext from the ciphertext seen in the communication channel. The decryption algorithm may be known to the attacker but for the message to be decrypted, the decryption key must also be known. Keys therefore add another layer of security to a message.
There are two general types of key-based algorithms: symmetric and asymmetric key encryption. The relationship between the encryption and decryption keys is the crucial difference between the two cryptosystems. Whilst the keys do not have to be the same, it is practically impossible to decrypt the ciphertext if an unrelated encryption key is used. Hence the keys must be closely associated.
Written by JaneW
