
To implement RSA within python, we have put together a tutorial to talk you though how to code an RSA function:
 This function generates a pair of random RSA keys with a modulus of nBits bits. It does this by generating 2 random primes so that their product (the modulus) has the required size and the primes vary in size by a random number of bits. It then randomly generates the public key's power and increments it until it is coprime to the product of p-1 and q-1 where p and q are the primes generated earlier. Finallly it calculates the private key's power by finding the multiplicative inverse of e (the public key's power) mod (p-1)*(q-1). It returns the public key's power, the private key's power and the modulus in an array.
Parameters:
• nBits - An integer that specifies the required number of bits for the modulus. If unspecified it has a default value of 2048 and if too small (less than 8) then it is replaced by this value.
The returned value is an array containing the public key's power, the private key's power and the modulus respectively.
Other functions from this module used:
• GetRandomPrime
• hcf
• inv_mod
This function generates a pair of random RSA keys with a modulus of nBits bits. It does this by generating 2 random primes so that their product (the modulus) has the required size and the primes vary in size by a random number of bits. It then randomly generates the public key's power and increments it until it is coprime to the product of p-1 and q-1 where p and q are the primes generated earlier. Finallly it calculates the private key's power by finding the multiplicative inverse of e (the public key's power) mod (p-1)*(q-1). It returns the public key's power, the private key's power and the modulus in an array.
Parameters:
• nBits - An integer that specifies the required number of bits for the modulus. If unspecified it has a default value of 2048 and if too small (less than 8) then it is replaced by this value.
The returned value is an array containing the public key's power, the private key's power and the modulus respectively.
Other functions from this module used:
• GetRandomPrime
• hcf
• inv_mod
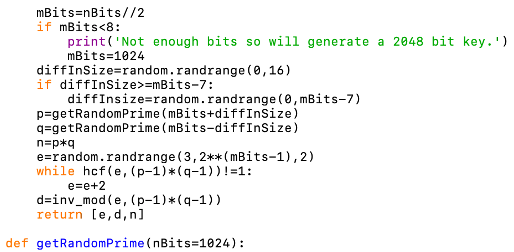 This function generates a random prime that is nBits bits in size. For small primes (at most 256 bits) it does this by repeatedly generating a random odd number of the required size and checking if it's prime. For larger primes it does this by generating a random range (of size 2^16) of numbers of the required size and finding the first prime in this range.
Parameters:
• nBits - An integer specifying the size of the prime to be generated in bits. If unspecified it has a default value of 1024.
The returned value is the generated prime.
Other functions from this module used:
• sieve
This function generates a random prime that is nBits bits in size. For small primes (at most 256 bits) it does this by repeatedly generating a random odd number of the required size and checking if it's prime. For larger primes it does this by generating a random range (of size 2^16) of numbers of the required size and finding the first prime in this range.
Parameters:
• nBits - An integer specifying the size of the prime to be generated in bits. If unspecified it has a default value of 1024.
The returned value is the generated prime.
Other functions from this module used:
• sieve
 This function encrypts a given string with the RSA key (power and modulus) provided. It applies padding to the string first if required and will remove the end of the string if it is too long to be encrypted by the modulus without loss of information.
Parameters:
• text - A string containing the text to be encrypted.
• power - An integer that is the RSA key's power.
• modulus - An integer that is the RSA key's modulus.
• padding - A Boolean specifying whether or not to add padding. If unspecified it will have a default value of True.
The returned value is the encrypted string.
Other functions from this module used:
• numBits
• pad
• StrToInt
• power_mod
• IntToStr
This function encrypts a given string with the RSA key (power and modulus) provided. It applies padding to the string first if required and will remove the end of the string if it is too long to be encrypted by the modulus without loss of information.
Parameters:
• text - A string containing the text to be encrypted.
• power - An integer that is the RSA key's power.
• modulus - An integer that is the RSA key's modulus.
• padding - A Boolean specifying whether or not to add padding. If unspecified it will have a default value of True.
The returned value is the encrypted string.
Other functions from this module used:
• numBits
• pad
• StrToInt
• power_mod
• IntToStr
 This function decrypts the given string with the RSA key (power and modulus) provided. It removes any padding after the decryption if required.
Parameters:
• text - A string containing the text to be decrypted.
• power - An integer that is the RSA key's power.
• modulus - An intger that is the RSA key's modulus.
• padding - A Boolean specifying whether or not to remove padding. If unspecified it will have a default value of True.
The returned value is the decrypted string.
Other functions in this module used:
• numBits
• StrToInt
• power_mod
• IntToStr
• removePadding
This function decrypts the given string with the RSA key (power and modulus) provided. It removes any padding after the decryption if required.
Parameters:
• text - A string containing the text to be decrypted.
• power - An integer that is the RSA key's power.
• modulus - An intger that is the RSA key's modulus.
• padding - A Boolean specifying whether or not to remove padding. If unspecified it will have a default value of True.
The returned value is the decrypted string.
Other functions in this module used:
• numBits
• StrToInt
• power_mod
• IntToStr
• removePadding
 This function adds PKCS1 v1.5 padding to the given text so that the text is the required block size. That is it adds padding starting with the hex 0002 and ending with the hex ffff to the begining of the string. The rest of the padding is random and does not contain the hex sequence ffff.
Parameters:
• text - A string containing the text to be padded.
• block_size - An integer specifying the required size of the padded text.
The returned value is the padded text.
This function adds PKCS1 v1.5 padding to the given text so that the text is the required block size. That is it adds padding starting with the hex 0002 and ending with the hex ffff to the begining of the string. The rest of the padding is random and does not contain the hex sequence ffff.
Parameters:
• text - A string containing the text to be padded.
• block_size - An integer specifying the required size of the padded text.
The returned value is the padded text.
 This function removes PKCS1 padding from the given text. If it does not have valid padding the function returns an empty string.
Parameters:
• text - A string containing the text to remove the padding from.
The returned value is the text with the padding removed or an empty string.
This function removes PKCS1 padding from the given text. If it does not have valid padding the function returns an empty string.
Parameters:
• text - A string containing the text to remove the padding from.
The returned value is the text with the padding removed or an empty string.
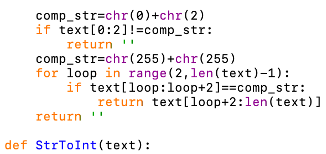 This function turns a string into an integer. It does this by iterating through each character in the string, converting it to its extended ASCII value and adding this to a running total by first multiplying by 256 to the power of the number of places from the end of the string the character is. This assigns each string a unique integer.
Parameters:
• text - The string to be turned into an integer.
The returned value is the integer produced from the string.
This function turns a string into an integer. It does this by iterating through each character in the string, converting it to its extended ASCII value and adding this to a running total by first multiplying by 256 to the power of the number of places from the end of the string the character is. This assigns each string a unique integer.
Parameters:
• text - The string to be turned into an integer.
The returned value is the integer produced from the string.
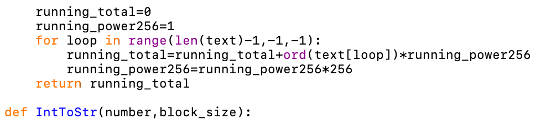 This function turns an integer into a string. It does this by finding the remainder of the current number (initialised to the given integer) divided by 256, adding the character relating to this remainder (using extended ASCII) to the begining of a string (initialised to an empty string) and then replaces the current number with itself divided (integer division) by 256. It repeats this process until a string of the required length is produced.
Parameters:
• number - The integer to be turned into a string.
• block_size - An integer specifying the required length of the produced string.
The returned value is the string produced from the number.
This function turns an integer into a string. It does this by finding the remainder of the current number (initialised to the given integer) divided by 256, adding the character relating to this remainder (using extended ASCII) to the begining of a string (initialised to an empty string) and then replaces the current number with itself divided (integer division) by 256. It repeats this process until a string of the required length is produced.
Parameters:
• number - The integer to be turned into a string.
• block_size - An integer specifying the required length of the produced string.
The returned value is the string produced from the number.
 This function calculates the number of bits required to represent a given integer.
Parameters:
• number - The integer to calculate the number of bits for.
The returned value is the number of required bits.
This function calculates the number of bits required to represent a given integer.
Parameters:
• number - The integer to calculate the number of bits for.
The returned value is the number of required bits.
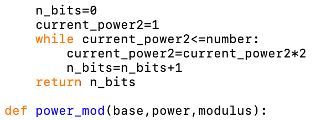 This function calculates a number to a given power modulo (the remainder when divided by) a given modulus. It does this efficiently by repeatedly squaring the given number, if the current power number is odd it multiplies a running value (initialised to 1) by the current squared value and divides the current power value by 2 (integer division). Every operation is performed in modular arithmetic (using the remainders when divided by the given modulus) to improve efficiency.
Parameters:
• base - An integer that is the base for the exponentiation.
• power - An integer that is the power to raise base to.
• modulus - An integer that is the number to divide by to calculate the remainders.
The returned value is basepower (mod modulus).
This function calculates a number to a given power modulo (the remainder when divided by) a given modulus. It does this efficiently by repeatedly squaring the given number, if the current power number is odd it multiplies a running value (initialised to 1) by the current squared value and divides the current power value by 2 (integer division). Every operation is performed in modular arithmetic (using the remainders when divided by the given modulus) to improve efficiency.
Parameters:
• base - An integer that is the base for the exponentiation.
• power - An integer that is the power to raise base to.
• modulus - An integer that is the number to divide by to calculate the remainders.
The returned value is basepower (mod modulus).
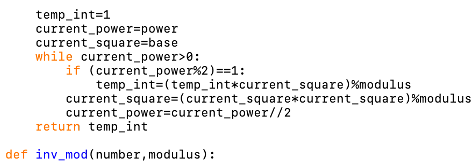 This function calculates the multiplcative inverse of a given number with a given modulus (when a number and its inverse are multiplied the remainder when divided by the modulus is 1). It does this using the extended Euclidean algorithm to find 2 numbers a and b such that a * number + b * modulus = 1. In this formula the number a is the inverse of number for the given modulus. This function assumes that the inverse exists (i.e. the given number and modulus are coprime).
Parameters:
• number - The integer to find the multiplicative inverse of.
• modulus - The integer that is the modulus to find the inverse of number for.
The returned value is the multiplicative inverse of the given number for the given modulus.
Other functions from this module used:
• extendedhcf
This function calculates the multiplcative inverse of a given number with a given modulus (when a number and its inverse are multiplied the remainder when divided by the modulus is 1). It does this using the extended Euclidean algorithm to find 2 numbers a and b such that a * number + b * modulus = 1. In this formula the number a is the inverse of number for the given modulus. This function assumes that the inverse exists (i.e. the given number and modulus are coprime).
Parameters:
• number - The integer to find the multiplicative inverse of.
• modulus - The integer that is the modulus to find the inverse of number for.
The returned value is the multiplicative inverse of the given number for the given modulus.
Other functions from this module used:
• extendedhcf
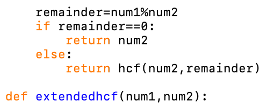
 This function calculates the highest common factor of 2 given integers. It does this using the Euclidean algorithm.
Parameters:
• num1 - One of the integers to calculate the highest common factor of.
• num2 - The other integer to calculate the highest common factor of.
The returned value is the highest common factor of the given numbers.
This function calculates the highest common factor of 2 given integers. It does this using the Euclidean algorithm.
Parameters:
• num1 - One of the integers to calculate the highest common factor of.
• num2 - The other integer to calculate the highest common factor of.
The returned value is the highest common factor of the given numbers.
 This function calculates the highest common factor of 2 given integers and finds a linear combination of the 2 numbers that equals this value. It does this using the extended Euclidean algorithm.
Parameters:
• num1 - One of the integers to calculate the highest common factor of.
• num2 - The other integer to calculate the highest common factor of.
The returned value is an array of integers [a,b,c] where a * num1 + b * num2 = c and c is the highest common factor of num1 and num2.
This function calculates the highest common factor of 2 given integers and finds a linear combination of the 2 numbers that equals this value. It does this using the extended Euclidean algorithm.
Parameters:
• num1 - One of the integers to calculate the highest common factor of.
• num2 - The other integer to calculate the highest common factor of.
The returned value is an array of integers [a,b,c] where a * num1 + b * num2 = c and c is the highest common factor of num1 and num2.
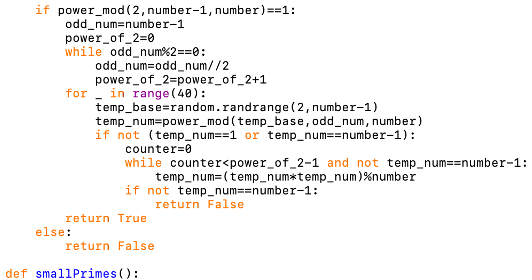
 This function tests a given integer for primality. It does this by a Fermat test with base 2 and a 40 round Miller-Rabin test. This function is probabilistic but the probability of failure is negligible.
Parameters:
• number - The integer to test for primality.
The returned value is a Boolean specifying whether or not the given number is prime.
This function tests a given integer for primality. It does this by a Fermat test with base 2 and a 40 round Miller-Rabin test. This function is probabilistic but the probability of failure is negligible.
Parameters:
• number - The integer to test for primality.
The returned value is a Boolean specifying whether or not the given number is prime.
 This function creates an array of all primes less than 216.
This function creates an array of all primes less than 216.
 This function sieves a given range for multiples of small prime numbers (less than 216) and then finds the first prime in the remaining numbers. It returns a 0 if there are no primes in the given range.
Parameters:
• lower_bound - The smallest integer in the given range.
• size - The number of integers in the given range.
The returned value is the first prime in the range or 0 if there are no primes in the range.
This function sieves a given range for multiples of small prime numbers (less than 216) and then finds the first prime in the remaining numbers. It returns a 0 if there are no primes in the given range.
Parameters:
• lower_bound - The smallest integer in the given range.
• size - The number of integers in the given range.
The returned value is the first prime in the range or 0 if there are no primes in the range.
 This array of small prime numbers is used by the sieve function and is stored as a variable so that it does not need to be generated everytime a new large prime is needed.
sPrimes=smallPrimes()
Written by Abby
This array of small prime numbers is used by the sieve function and is stored as a variable so that it does not need to be generated everytime a new large prime is needed.
sPrimes=smallPrimes()
Written by Abby