Elliptic-Curve

In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form. which is non-singular; that is, the curve has no cusps or self-intersections. Elliptical curve cryptography (ECC) is a public key encryption technique based on elliptic curve theory that can be used to create faster, smaller, and more efficient cryptographic keys. ECC generates keys through the properties of the elliptic curve equation instead of the traditional method of generation as the product of very large prime numbers. 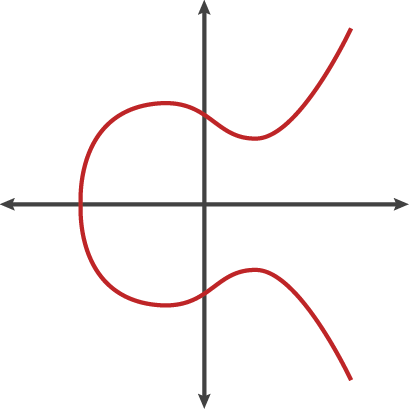Point Addition A straight line on the elliptic curve y² = x³ + ax + b intersects three times, each point of intersection is called P, Q and -R. P and Q can be used to find R, which is a reflection of point -R over the x axis. First the gradient (m) of the line is needed.

The gradient can then be used to find the x and y coordinates for R. Scalar Multiplication However when R = 2P, the formulae change, and m is now the gradient of the tangent of P. To find 3P you would need to first calculate 2P and then point addition for P + 2P. To find 4P you would calculate 2P, and the 4P which is 2(2P). To find 5P you would need to first calculate 2P, then 4P and then 5P = 4P + P. You must remember these concepts to understand the Elliptic Curve Diffie Hellman Key Exchange. Key Generation Alice and Bob will agree on a, b and p (the modulus) to define their curve; note 4a³ + 27b ≠ 0. Alice and Bob then agree on the Generator point G which they will use to find their private keys. n is identified, where nG = (∞,∞), this is where x_(n-1)G = x_G. If for example 10G = G and 10 < n, then there are only 10 points on the curve. h is defined as h = number of points on the curve / n. All of the previously mentioned values are public and any interceptor can view these without knowing Alice and Bob’s secret key. Alice and Bob pick private keys α and β only accessible to themselves. Alice and Bob do not know each other's private keys. Alice and Bob can then exchange their public keys on an insecure channel, which are found using the following formulae: Alice and Bob can then find their shared secret key without knowing each other’s private keys using this formula: Example: Let a = 2, b = 2, p = 17, G = (5, 1) n = 19, h = 1. Alice chooses her private key α = 3 and calculates her private key A which equals 3G. Step 1: m = (3x_G2 + a) / 2y_G mod p = (3(5)2 + 2)/(2 * 1) mod 17 = 77 / 2 mod 17 [Use the Extended Euclidean Algorithm here] = 77 * 9 mod 17 = 13 x_2G = m2 - 2x_G mod p = 132 - 2*5 mod 17 = 159 mod 17 = 6 y_2G = m(x_G - x_2G ) - y_G mod p = 13(5 - 6) - 1 mod 17 = -14 mod 17 = 3 2G = (6, 3) Step 2: P = 2G, Q = G m = (y_2G - y_G) / (x_2G - x_G) mod p = (3 - 1) / (6 - 5) mod 17 = 2 * 1 = 2 x_3G = m2 - (x_2G + x_G) mod p = 22 - (6 + 5) mod 17 = 4 - 11 mod 17 = 10 y_3G = m(x_2G - x_G) - y_2G mod p = 2(6 - 5) - 3 mod 17 = 2 - 3 mod 17 = 16 3G = (10, 6) Written by Chelsea